ウォリス積分

\int_{0}^{\frac{π}{2}} \cos^{n} x d x

= \int_{0}^{\frac{π}{2}} \sin^{n} x d x

= \{\begin{matrix} \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \dots \frac{1}{2} \cdot \frac{π}{2} \\ \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \dots \frac{2}{3} \cdot 1 \end{matrix}

n

：偶数

n

：奇数

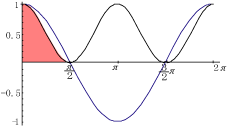
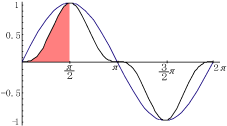
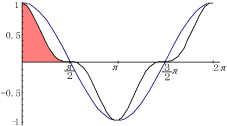
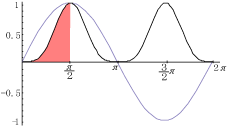
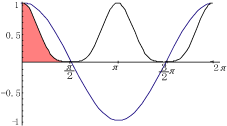
この積分は，下図の赤の領域の面積を求めていることになる．
積分区間が0から $\frac{π}{2}$ でない場合は，周期性，対称性に注意して適用すること．

${sin}^{2} x$ のグラフ（青線： $sin x$ ）	${cos}^{2} x$ のグラフ（青線： $cos x$ ）
${sin}^{3} x$ のグラフ（青線： $sin x$ ）	${cos}^{3} x$ のグラフ（青線： $cos x$ ）
${sin}^{4} x$ のグラフ（青線： $sin x$ ）	${cos}^{4} x$ のグラフ（青線： $cos x$ ）

■計算例

$\int_{0}^{\frac{π}{2}} \sin^{5} x d x$ $= \frac{4}{5} \cdot \frac{2}{3} \cdot 1$ $= \frac{8}{15}$

$\int_{0}^{\frac{π}{2}} \sin^{6} x d x$ $= \frac{5}{6} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{π}{2}$ $= \frac{5 π}{32}$

$\int_{0}^{2 π} {cos}^{4} x d x$ $= 4 \int_{0}^{\frac{π}{2}} {cos}^{4} x d x$ $= 4 \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{π}{2} = \frac{3 π}{4}$

$\int_{- \frac{π}{2}}^{\frac{π}{2}} {cos}^{3} x d x$ $= 2 \int_{0}^{\frac{π}{2}} {cos}^{3} x d x = 2 \cdot \frac{2}{3} \cdot 1 = \frac{4}{3}$

$\int_{0}^{π} {sin}^{3} x d x$ $= 2 \int_{0}^{\frac{π}{2}} {sin}^{3} x d x = 2 \cdot \frac{2}{3} \cdot 1 = \frac{4}{3}$

■式の導出

$\int_{0}^{\frac{π}{2}} {sin}^{n} x d x = I_{n}$

とおく．部分積分によって

$\begin{array}{l} I_{n} & = \int_{0}^{\frac{π}{2}} (sin x) ({sin}^{n - 1} x) d x \\ = {[(- cos x) ({sin}^{n - 1} x)]}_{0}^{\frac{π}{2}} - \int_{0}^{\frac{π}{2}} (- cos x) (n - 1) ({sin}^{n - 2} x) cos x d x \\ = (n - 1) \int_{0}^{\frac{π}{2}} ({cos}^{2} x) ({sin}^{n - 2} x) d x \\ = (n - 1) \int_{0}^{\frac{π}{2}} (1 - {sin}^{2} x) ({sin}^{n - 2} x) d x \\ = (n - 1) \int_{0}^{\frac{π}{2}} ({sin}^{n - 2} x) d x - (n - 1) \int_{0}^{\frac{π}{2}} {sin}^{n} x d x \\ = (n - 1) I_{n - 2} - (n - 1) I_{n} \end{array}$

となる．よって，漸化式

$\begin{array}{l} I_{n} = (n - 1) I_{n - 2} - (n - 1) I_{n} \\ I_{n} = \frac{n - 1}{n} I_{n - 2} \end{array}$

が得られる．

$I_{0} = \int_{0}^{\frac{π}{2}} d x = \frac{π}{2}$ 　， $I_{1} = \int_{0}^{\frac{π}{2}} sin x d x = {[- cos x]}_{0}^{\frac{π}{2}} = 1$

であるので

$I_{n} = \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{1}{2} \cdot \frac{π}{2}$ 　　（ $n$ が偶数の場合）

$I_{n} = \frac{n - 1}{n} \cdot \frac{n - 3}{n - 2} \cdot \dots \cdot \frac{2}{3} \cdot 1$ 　　（ $n$ が奇数の場合）

となる．次に

$\int_{0}^{\frac{π}{2}} {cos}^{n} x d x$ 　を求める．

$sin x = cos (\frac{π}{2} - x)$ なので，置換積分を使って $\int_{0}^{\frac{π}{2}} {sin}^{n} x d x$ の結果を利用する．

$\frac{π}{2} - x = t$ $(\frac{d t}{d x} = - 1 \to d x = - d t)$ とおくと， $x = 0 \to t = \frac{π}{2}$ ， $x = \frac{π}{2} \to t = 0$ となるので

$\int_{0}^{\frac{π}{2}} {sin}^{n} x d x = \int_{0}^{\frac{π}{2}} cos {(\frac{π}{2} - x)}^{n} x d x$ $= \int_{\frac{π}{2}}^{0} {cos}^{n} t (- d t)$ $= \int_{0}^{\frac{π}{2}} \cos^{n} t d t$

と計算できる．

定積分であるので，積分変数を $t$ から $x$ に書き換えても積分の値は変わらない．

と計算できる．よって

$\int_{0}^{\frac{π}{2}} \cos^{n} t d t = \int_{0}^{\frac{π}{2}} \cos^{n} x d x$

となる．したがって

$\int_{0}^{\frac{π}{2}} \cos^{n} x d x = \int_{0}^{\frac{π}{2}} \sin^{n} x d x$

となる．

ホーム>>カテゴリー分類>>積分>>積分の具体事例>>三角関数（正弦，余弦，正接）の積分>>積分　(sinx )^n 　(cosx )^n

最終更新日： 2024年8月19日